ORB-SLAM2 Notes: Day 9 – KeyPoint Orientation - Pinecone Log

In the last article, KeyPoint Distribution, I showed the QuadTree class code and the KeyPoint Distribution algorithm. Next we will compute the orientation for each keypoint to achieve rotation invariance.

The KeyPoint Orientation code has been uploaded to my GitHub repository. Readers are welcome to view it.

KeyPoint Orientation

The article, Techniques of KeyPoint Extraction, mentions that descriptors are used for matching keypoints from different images. Before computing the descriptor for a keypoint, its intensity centroid is used to determine the orientation, accounting for camera rotation.

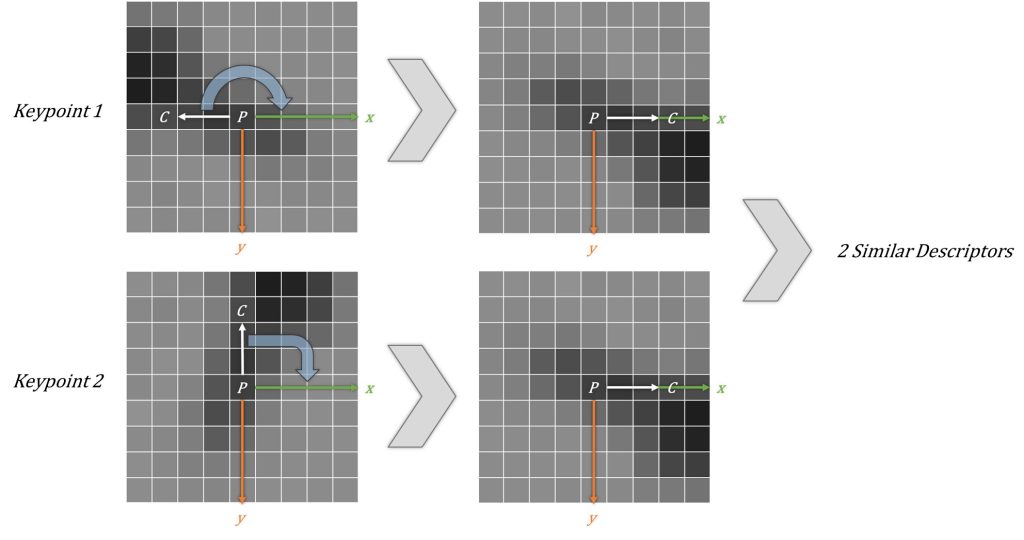
Fig. 1. Two matched keypoints have similar descriptors determined by their orientations. P indicates the coordinate of a keypoint, and C indicates the intensity centroid of a keypoint.

Compute Orientation

Preparation

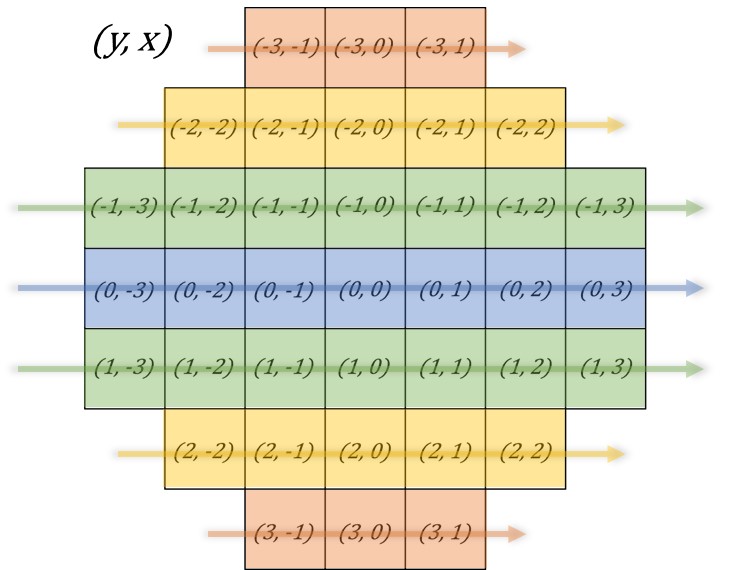
Before calculating orientation, it’s important to set a radius, for example, 31 as in ORB-SLAM2. Next I will use a radius of 3 as shown in Fig. 2 to explain this process for simplicity.

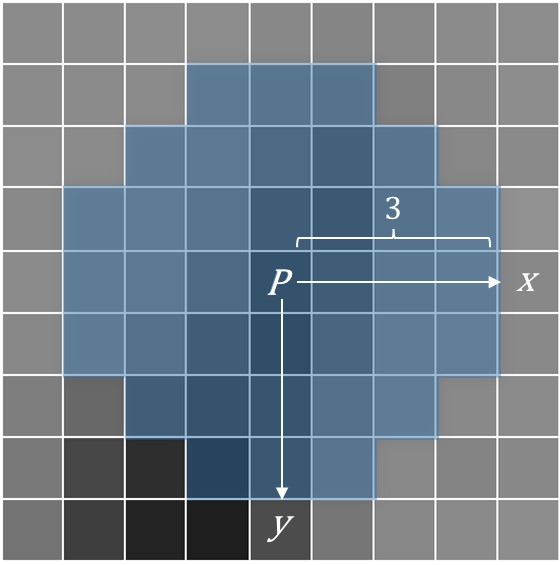
Fig. 2. Circular area with a radius of 3 for simplicity.

Each coordinate, relative to center P(y, x), has an intensity value from 0 to 255. — Fig. 3. Each coordinate, relative to center P(y, x),
has an intensity value from 0 to 255.

Calculation

Vector from P to C

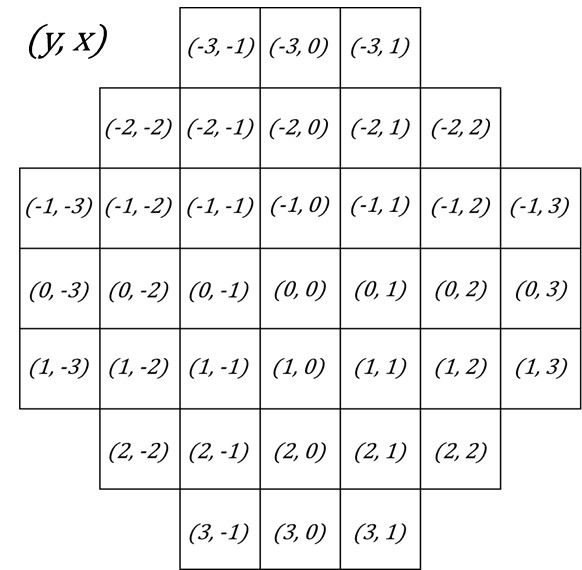
Each coordinate, shown in Fig. 3, is multiplied by its intensity value, referred to as its weight; the weighted coordinates are then summed.

$$ k\vec{PC} = k[C_y,C_x] = \sum_{y=-3}^{y=3} \sum_{x=-3}^{x=3} W_{yx} \cdot \vec{P}_{yx} \tag{1} $$

In equation (1), $ k $ is a constant; $ \vec{PC} $ represents the vector from $P$ to intensity centroid; $ [C_y,C_x] $ represents the centroid coordinate; $ W_{yx} $ represents the intensity at $ (y,x) $, and $ \mathbf{P}_{yx} $ represents a vector $ [y,x] $.

Note that the area is circular rather than square.

Orientation

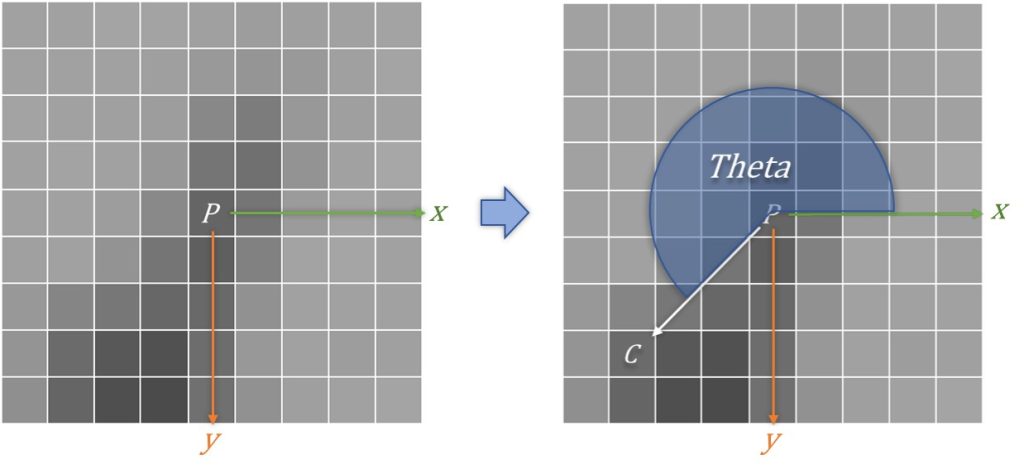
The intensity centroid determines the $ \theta \in [0^\circ, 360^\circ] $, as shown in Fig. 4, using the following equation:

$$
\theta =
\arctan\frac{C_y}{C_x}
\in [-90^\circ, 90^\circ]
\tag{2}
$$

In equation (2), $180^\circ$ should be added to $\theta$ to ensure $ \theta \in [0^\circ, 360^\circ] $ if $C_x < 0$.

ORB-SLAM2 Notes: Day 9 – KeyPoint Orientation

Table of Contents

KeyPoint Orientation