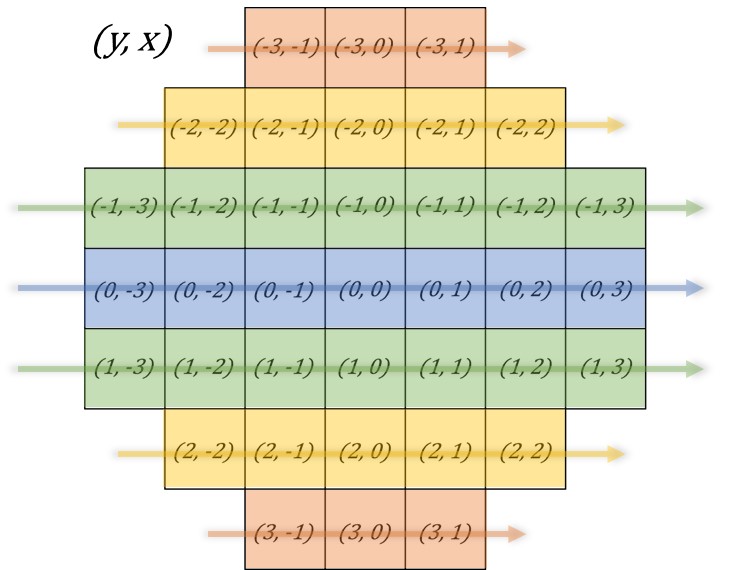
In the last article, I implemented Orientation Computer, which computes orientations of keypoints. Next we will use orientation info to compute descriptors for matching keypoints across frames.
The code is available on my GitHub repository, and readers are welcome to check it out!
Table of Contents
Descriptor
Overview
In ORB-SLAM2, we use descriptors to match keypoints across frames, which makes spatial localization possible using triangulation, as shown in Fig. 1.

Structure
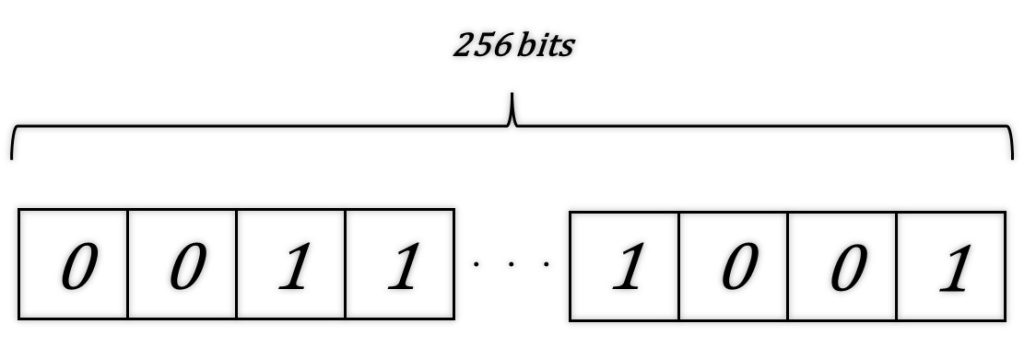
In fact, a descriptor is a 256-bit data structure, where each bit represents either 0 or 1, as shown in Fig. 2.
Match
We use Hamming distance to evaluate similarity between two descriptors. It is computed by counting the number of differing corresponding bits. The smaller the distance, the more similar the two descriptors are.
Hamming Distance
A simple example: consider two 8-bit binary descriptors, \(d_1\) and \(d_2\):
$$
d_1 = 10\underline110\underline010 \\
d_2 = 10\underline010\underline110
$$
There are two differing bits, so the Hamming distance is 2.
How to Compute Descriptor?
Coordinate Rotation
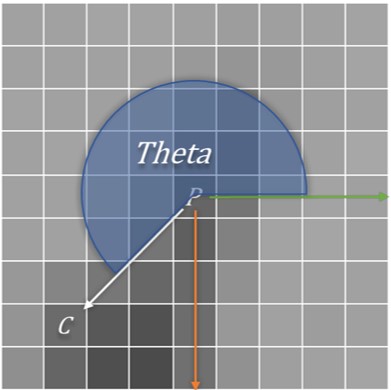
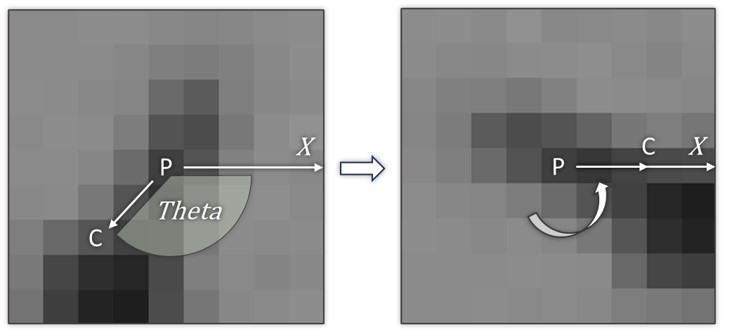
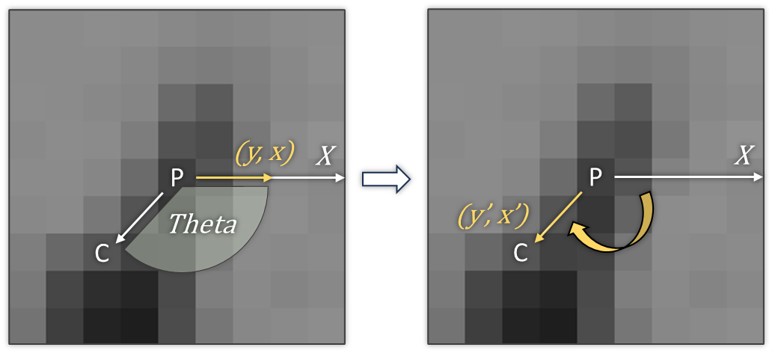
After getting the orientation of a keypoint, we use it to compute the descriptor. First, it is necessary to rotate the keypoint so that its orientation aligns with the x-axis as shown in Fig. 3, which can be indirectly achieved by rotating the original sample coordinates according to orientation, as shown in Fig. 4.
$$
\begin{bmatrix} x’ \\ y’ \end{bmatrix} =
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\begin{bmatrix} x \\ y \end{bmatrix}
\tag{1}
$$
Using the orientation information compensates for camera rotation and makes computed descriptors more robust.
Gaussian Blur
Blurring the image before computing descriptors helps reduce noise.
Compute Descriptor
In the circular region of radius 15 around the keypoint, we randomly select 256 pairs of pixels, and then compare two pixels’ intensities in each pair. Although I say “randomly”, there has been a template made by others that contains sorted pairs of coordinates. We just need to compute descriptors based on it.
Consider one bit of a descriptor, its value is:
$$
value =
\begin{cases}
1, & \text{if } I(y_1,x_1) < I(y_2,x_2) \\
0, & \text{if } I(y_1,x_1) \ge I(y_2,x_2)
\end{cases}
\text{ , where $I(y,x)$ represents the intensity at this point. }
$$
By repeating this process, we will obtain the 256-bit descriptor representing the information around the keypoint.