In the last article, I explained the concept of keypoint orientation. Now, let’s implement the algorithm to compute it. The code is available on my GitHub repository, and readers are welcome to check it out!
Table of Contents
OrientationComputer.h
#ifndef ORIENTATIONCOMPUTER_H
#define ORIENTATIONCOMPUTER_H
#include <vector>
#include <opencv2/core.hpp>
#include <opencv2/features2d.hpp>
using namespace cv;
using namespace std;
namespace my_ORB_SLAM2 {
class OrientationComputer {
public:
/*
@brief Before calculating orientation, it’s important to set a radius.
@param[in] iRadius: Radius of the circular area. */
OrientationComputer(int iRadius);
~OrientationComputer() {};
// Radius of the circular area.
int miRadius;
// Half the number of points per unit along the y-axis of the circular area.
int nHalfPointsPerY[16] = {15,15,15,15,14,14,14,13,13,12,11,10,9,8,6,3};
/*
@brief Compute a keypoint's orientation.
@param[in] keyPoint: The target keypoint.
@param[in] image: The image that contains the keypoint. */
inline float getOrientation(KeyPoint &keyPoint, const Mat &image);
/*
@brief Compute orientation for each keypoint from an image pyramid.
@param[in] vvKeyPointsPerLevel: Keypoints detected at each pyramid level.
@param[in] vImagePerLevel: Images at each pyramid level. */
void compute(
vector<vector<KeyPoint>> &vvKeyPointsPerLevel,
const vector<Mat> &vImagePerLevel
);
};
}
#endifOrientationComputer.cpp
#include "myORB-SLAM2/OrientationComputer.h"
namespace my_ORB_SLAM2 {
/*
@brief Before calculating orientation, it’s important to set a radius.
@param[in] iRadius: Radius of the circular area. */
OrientationComputer::OrientationComputer(int iRadius): miRadius(iRadius) {}
/*
@brief Compute a keypoint's orientation.
@param[in] keyPoint: The target keypoint.
@param[in] image: The image that contains the keypoint. */
inline float OrientationComputer::getOrientation(KeyPoint &keyPoint, const Mat &image) {
// Get the pointer to the center of the circular area.
const uchar* pCenter = &image.at<uchar>(keyPoint.pt.y, keyPoint.pt.x);
// Width of the image.
int nCols = image.cols;
// Sum of weighted coordinates.
int weightedSumY = 0;
int weightedSumX = 0;
// Accumulate weighted coordinates along the center row.
for(int iX = -nHalfPointsPerY[0]; iX <= nHalfPointsPerY[0]; ++iX) {
weightedSumX += pCenter[iX] * iX;
}
// Process the upper and lower halves of the circular area.
for(int iY = 1; iY <= miRadius; ++iY) {
// Accumulate the weights temporarily along row iY and -iY.
int tempSumY = 0;
// Byte offset from center row to row iY.
int nMove = nCols * iY;
// Accumulate weighted coordinates symmetrically along rows iY and -iY.
for(int iX = -nHalfPointsPerY[iY]; iX <= nHalfPointsPerY[iY]; ++iX) {
// Intensity values at symmetric pixels.
int weightDown = pCenter[iX - nMove];
int weightUp = pCenter[iX + nMove];
// The code below is equivalent to accumulating "weightUp * [iY, iX] + weightDown * [-iY, iX]".
// Here, (weightUp - weightDown) is not multiplied by iY in each loop iteration.
tempSumY += weightUp - weightDown; // Origin code: tempSumY += iY * weightUp - iY * weightDown;
weightedSumX += iX * (weightUp + weightDown);
}
// Multiply only once to accelerate computation.
weightedSumY += tempSumY * iY;
}
// Return the orientation(0 ~ 360 degrees).
return fastAtan2(weightedSumY, weightedSumX);
}
/*
@brief Compute orientation for each keypoint from an image pyramid.
@param[in] vvKeyPointsPerLevel: Keypoints detected at each pyramid level.
@param[in] vImagePerLevel: Images at each pyramid level. */
void OrientationComputer::compute(
vector<vector<KeyPoint>> &vvKeyPointsPerLevel,
const vector<Mat> &vImagePerLevel
) {
// Iterate over each level of the pyramid.
for(int iLevel = 0; iLevel < vImagePerLevel.size(); ++iLevel) {
// The image and keypoints at this level.
const Mat &image = vImagePerLevel[iLevel];
vector<KeyPoint> &vKeyPoints = vvKeyPointsPerLevel[iLevel];
// The number of keypoints.
int nKeyPoints = vKeyPoints.size();
// Compute the orientation for each keypoint.
for(int i = 0; i < nKeyPoints; ++i)
vKeyPoints[i].angle = getOrientation(vKeyPoints[i], image);
}
}
} // my_ORB_SLAM2Details
Radius
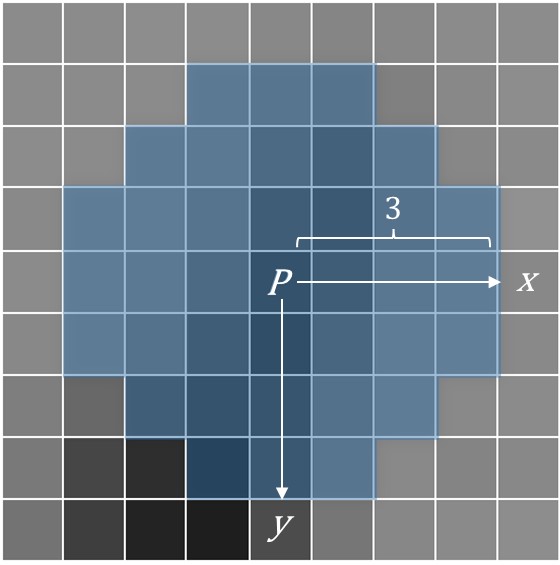
An Orientation Computer calculates the orientation of a keypoint with a given radius as shown in Fig. 1. In fact, don’t set a radius above or below 15, the former makes the computation inefficient; the latter reduces the accuracy of the computed orientation.
Symmetry
ORB-SLAM2 uses the symmetry of a circular area to accelerate the computation. For example, it accumulates weighted coordinates symmetrically along the rows y and -y, which reduces the number of multiplications and iterations.

...
// Accumulate weighted coordinates along the center row.
for(int iX = -nHalfPointsPerY[0]; iX <= nHalfPointsPerY[0]; ++iX) {
weightedSumX += pCenter[iX] * iX;
}
...
// Accumulate weighted coordinates symmetrically along rows iY and -iY.
for(int iX = -nHalfPointsPerY[iY]; iX <= nHalfPointsPerY[iY]; ++iX) {
// Intensity values at symmetric pixels.
int weightDown = pCenter[iX - nMove];
int weightUp = pCenter[iX + nMove];
// The code below is equivalent to accumulating "weightUp * [iY, iX] + weightDown * [-iY, iX]".
// Here, (weightUp - weightDown) is not multiplied by iY in each loop iteration.
tempSumY += weightUp - weightDown; // Origin code: weightedSumY += iY * weightUp - iY * weightDown;
weightedSumX += iX * (weightUp + weightDown);
}
// Multiply only once to accelerate computation.
weightedSumY += tempSumY * iY;
...Outcome
On my laptop, computing the orientation for 1,200 keypoints in one frame based on symmetry took about 0.000462 s. It is extremely fast, but the performance may vary slightly on other devices.

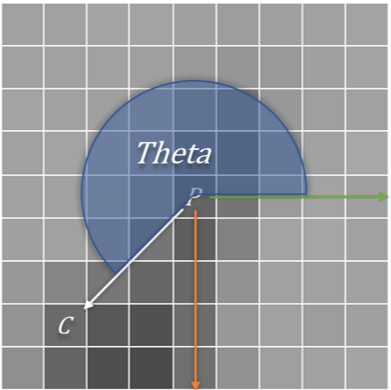

[…] the last article, I implemented Orientation Computer, which computes orientations of keypoints. Next we will use […]